Всем привет!
Не знаю как вы, но я люблю инфографики и статистические данные. С помощью них человек может получить максимальное количество информации за минимальное время. Главное — понимать, что за понятия здесь используются. Например, достаточно часто в статистике используется «среднее значение»: средняя зарплата, средняя продолжительность жизни, средний уровень интеллекта 🙂 и т.д. Сегодня мы посмотрим на сколько обманчивым может быть описание данных с помощью среднего.
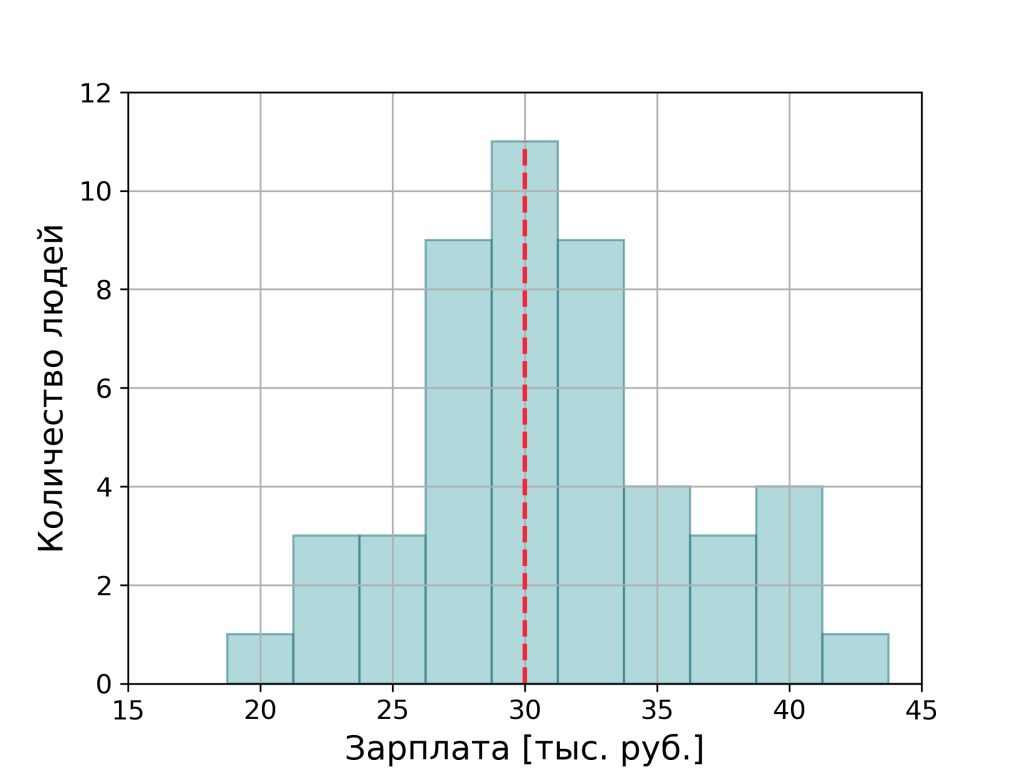
Итак, предположим, сижу я в кинозале. Фильм настолько скучный, что уснуть заняться статистическими расчётами оказалось куда интересней. Решила я подсчитать среднюю зарплату людей в зале. Для этого спросила каждого из 50-ти зрителей, сколько он получает. В результате выяснилось, что 11 человек получают около 30 тыс., 10 человек — 28 тыс., 10 человек — 32 тыс. и т.д. Теперь я могу построить график, отображающий сколько людей получает 20 тыс., 22.5 тыс., 30 тыс. и т.д. :
Кстати, заметьте, величина заработной платы, скорее всего, будет подчиняться распределению Гаусса, о котором мы говорили совсем недавно. Ну а теперь, для того чтобы описать эту группу людей, я подсчитаю среднее значение. Это делается очень просто: складываю зарплаты всех сидящих в зале и делю эту сумму на количество людей. То есть, например, если бы у нас было только 5 человек с зарплатами 30, 30, 25, 28, 15 тысяч рублей, то среднее значение бы равнялось (30+30+25+28+15)/5 = 25.6 тыс. руб. Для группы людей в кинозале я получила среднюю зарплату около 30 тыс. руб. Судя по графику выше, результат выглядит вполне себе логично.
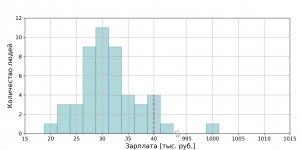
Всё бы ничего, но в середине сеанса в зал заходит продюсер фильма. И вот его зарплата ну уж очень сильно отличается от средней. Предположим, зарабатывает он миллион рублей в месяц. Что же тогда происходит с только что подсчитаной средней зарплатой по кинозалу? Она смещается, при чём смещается очень сильно. Теперь средняя зарплата равна 40 тыс. рублей:
Ну а вот этот результат, мне уже совсем не нравится. Ведь он противоречит тому, что я вижу. По моим ощущениям средняя зарплата по кинозалу не должна быть намного больше 30 тысяч. Но математика говорит иначе. Неужели она лжёт? Нет. Просто в данном случае использовать среднее значение неправильно. Более разумно в этом случае бы было использовать медиану.
Итак, что же это такое? Снова рассмотрим пример с зарплатами пяти человек: 30, 30, 25, 28, 15 тысяч рублей. Чтобы найти медиану нужно эти данные записать в порядке возрастания: 15, 25, 28, 30, 30. Теперь число, находящееся в середине этой последовательности, является медианой (это 28). То есть мне совершенно неважно, равна ли самая большая зарплата этих пятирых 30 тысячам или миллиону. Медиана останется равной 28 тысячам. И она будет более правдоподобно описывать данную группу. Таким же образом я считаю медиану заработной платы людей в кинозале. Даже после прихода продюсера фильма, медиана окажется около 30 тысяч рублей.
То есть описание заработной платы группы людей медианой в нашем случае дало более реальную оценку в сравнении со средним значением. Вот такая вот простая описательная статистика. Так что будьте внимательны к тому, что скрывается за высокопарными статистическими данными и подписывайся на мой телеграм-канал. Вопросы пишите в комментариях. Ну а если статья понравилась, обязательно поделись ссылкой с друзьями в социальных сетях :).