Привет всем!
Сегодня речь пойдёт о анализе данных. В этом разделе первым делом я хочу вас познакомить с распределением Гаусса (в народе известно как нормальное распределение). Не поверите, как много происходящего вокруг нас может быть описано этим законом.
Итак, давайте разбираться. Предположим, вы — владелец/а парикмахерской, и никак не можете решить сколько человек вам нужно нанять. Вы знаете, что в среднем к вам приходит подстричься человек шесть за час (ну да, крупная такая парикмахерская у вас), но случается, что приходит и 12 человек за час. «Cколько же парикмахеров мне нанять?» — думаете вы. Tут-то к вам на помощь и приходит Гаусс.
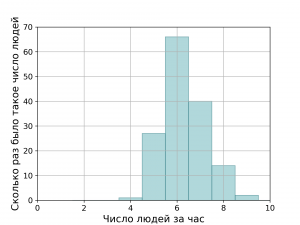
Но всё попорядку. Сначала придётся собрать данные. В течении нескольких недель мы будем записывать сколько клиентов было у нас каждый час. А затем построим вот такой график:
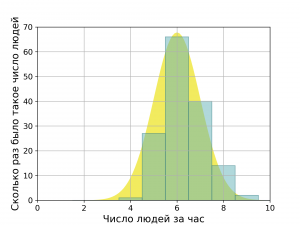
То есть, мы подсчитали сколько раз к нам за один час пришёл 1 человек, сколько раз — 2 человека, сколько раз — 3 человека, четыре, пять и т.д. Теперь эти данные можно описать вот такой вот кривой Гаусса:
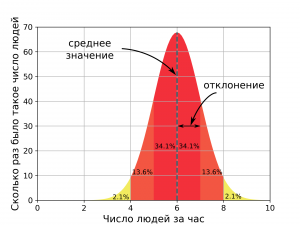
Такая кривая характеризуется всего двумя параметрами — средним значением и отклонением.
Среднее значение — это, по сути, то, что вы знали без всякого там Гаусса. Оно показывает, что чаще всего в вашей парикмахерской одновременно стригутся 6 человек. А вот отклонение — это тот параметр, который поможет вам решить, сколько людей необходимо иметь в штате. В нашем случае, отклонение равно единице. А это значит, что в 64.2% случаев одновременно в нашей парикмахерской стрижётся от 5 до 7 человек, а в 95.4% случаев — от 3 до 8 человек. Значит, чтобы удовлетворить запрос клиентов в 95.4% случаев в штате вы должны иметь 8 парикмахеров.
Такая оценка с помощью распределения Гаусса позволяет решать огромное число бизнес задач. Таким образом можно определять какое количество официантов должно работать в то или иное время; какое количество парковочных мест необходимо в торговом центре и т.д. Тут я оставляю простор для вашей фантазии и надеюсь, что вы подружитесь с Гауссом :).
Ах да, и не забудьте подписаться на мой телеграм-канал, чтобы быть всегда в курсе новостей.
Поделись заметкой с друзьями: