Всем привет!
Думаю, что каждый из нас хоть раз в жизни натыкался на формулу идеального веса. Знаете, такие формулы, когда подставляешь свой рост и вычисляешь какой вес тебе следовало бы иметь. Например, вес по формуле «мечта Лоренца» вычисляется следующим образом: РОСТ — 100 — (РОСТ — 150)/2. Подставляете свой рост в сантиметрах и готово. А задумывались ли вы, откуда эти формулы берутся и насколько близко к сердцу стоит принимать то, что ваш вес не совсем соответсвует идеальному? 🙂
Предполагаю, что такие формулы составляются очень просто. Для этого сначала собираются данные — рост и вес большого количества людей. А затем строится линейная регрессионная модель (ничего сложного, это та розовая прямая на рисунке).
Я взяла данные о росте и весе 200 людей здесь и провела прямую, которая наилучшим образом описывает эти данные. В результате, по моим предположениям, идеальный вес вычисляется по формуле: 0.6 · РОСТ — 50 (этой формулой задаётся розовая прямая). То есть, если я подсчитаю свой идеальный вес, то получу: ВЕС = 0.6 · 155 — 50 = 43 кг. И ура, я ему соответствую, ну или почти соответствую… :).
Если вы посмотрите на рисунок выше, то моя розовая прямая не так далека от прямой, описывающей «мечту Лоренца» (оранжевая прямая). Просто «мечта Лоренца» позволяет вам иметь больший вес. Короче говоря, формула идеального веса зависит от того, какие входные данные вы берёте. Поэтому не стоит расстраиваться из-за того, что ваш вес выше/ниже идеального, ведь всегда найдётся формула, где ваш сегодняшний вес окажется идеальным.
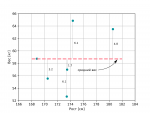
Ну а теперь давайте разберёмся, как же находится прямая, описывающая наши данные. Рассмотрим на примере шести человек, рост которых 173, 170, 173, 180, 169, 174 см и вес 60, 56, 53, 64, 59, 65 кг соответственно. Тогда средний вес вне зависимости от роста: (60 + 56 + 53 + 64 + 59 + 65)/5 = 59.5 кг. Нанесём эти данные на график:
Параметром, который оценивает насколько хорошо та или иная прямая описывает данные, является сумма квадратов расстояний от каждой точки до прямой. В нашем случае: 02 + 3.22 + 6.12 + 1.72 + 6.12 + 4.82 = 110.59. Теперь рассмотрим лучшую аппроксимацию (описание) наших данных:
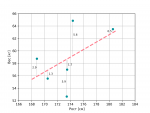
Здесь, оценка аппроксимации равна: 2.92 + 1.32 + 5.92 + 1.72 + 5.62 + 0.52 = 79.41. То есть прямая, которая лучше всего описывает наши данные, будет иметь наименьшую сумму квадратов расстояний от каждой точки до этой прямой. Такой метод называется методом наименьших квадратов и позволяет описать набор статистических данных с помощью прямой.
На этом сегодня всё, подписывайтесь на телеграм-канал Машин Learning там много чего интересного. И конечно же делитесь с друзьями ссылкой на данную статью в социальных сетях: