Всем привет!
Недавно на просторах википедии встретила мнемоническое стихотворение, позволяющее запомнить чему равно число е: «Экспоненту помнить способ есть простой: два и семь десятых, дважды Лев Толстой». Мне оно так понравилось, что я решила написать об этом числе статью. Сегодня расскажу откуда взялось число Эйлера. И имеет ли Эйлер к нему какое-то отношение.
Для начала только уточню при чём тут Лев Толстой. Дело в том, что он родился в 1828 году. А число е ≈ 2.718281828, вот и выходит дважды Лев Толстой. Для меня это крутая мнемоника, потому что теперь я знаю и чему равно число е и год рождения Льва Николаевича :).
Ну а теперь к самому числу. Предположим у вас есть лишний 1 ₽. И вы как разумный инвестор решаете вложить его в банк. Один из банков делает вам заманчивое предложение — 100% годовых, которые начисляются в конце года. То есть в результате вы получите 2 ₽. Пытаясь вас переманить, другой банк обещает те же самые проценты, но начисления будут производиться два раза в год. Это значит, что за первые полгода сумма вашего влада увеличится до 1 ₽· (1+0.5) = 1.5 ₽, а за год 1 ₽·(1+0.5)2 = 2.25 ₽. «Круто», — думаете вы — «может есть такой банк, который выплачивает те же самые 100%, но каждый месяц? Тогда я получу 1 ₽· (1+1/12)12 = 2.6₽ в конце года.»
В результате вы находите банк, который предлагает увеличивать частоту начисления процентов до тех пор, пока клиент их не остановит. Ну и в чём же тут подвох?
Итак, по сути мы не знаем сколько раз в год банк будет выплачивать проценты. Обозначим это количество за n. Тогда за год вклад увеличится до S = 1 ₽ · (1+1/n)n рублей. Так вот ещё в далёком 17 веке математик Якоб Бернулли вычислил, что предел такого процентного дохода равен 2.71828. Посмотрите на график: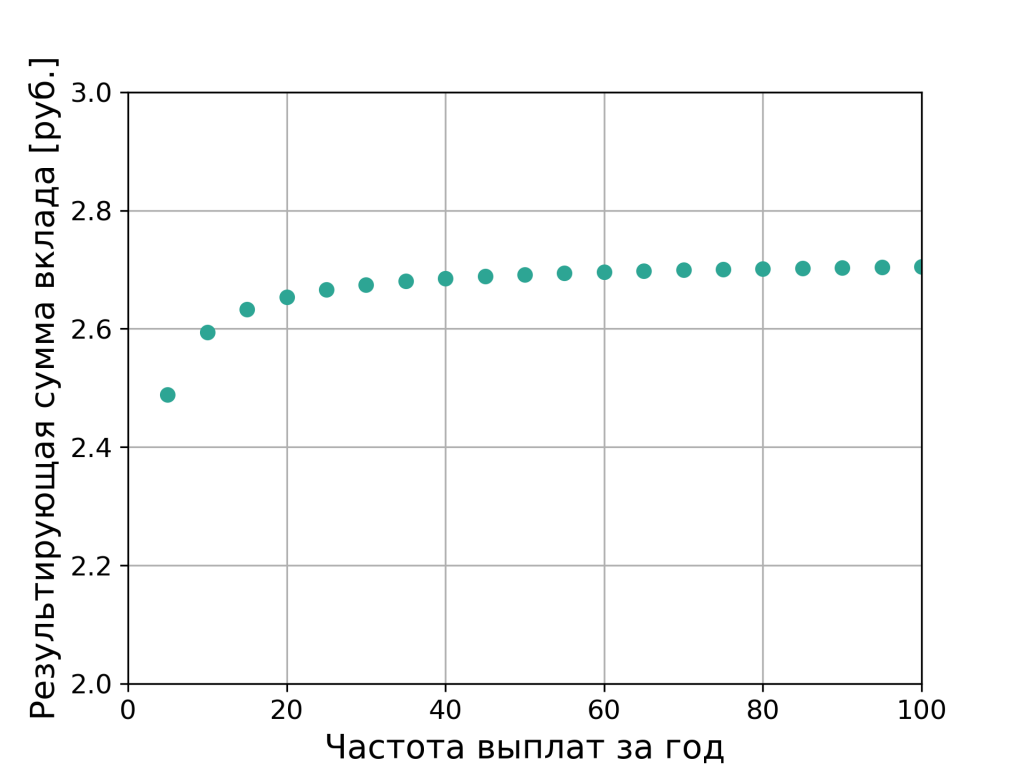
То есть максимальная сумма, которую вам выплатит банк при 100% годовых и максимальной частоте начисления процентов, не превысит 2.72₽.
Ну понятное дело, что 100% годовых ни в одном банке вы не получите. Все дают 8% — 9% годовых. Но например, чтобы выделится среди конкурентов, маркетологи вполне могут использовать слоган: «Бесконечная частота начисления процентов при 8% годовых». Ведь они точно знают, что от этого банк не разорится.
Да, как это связано с Эйлером? Эйлер начал первым обозначать константу 2.71828 буквой e. В результате, в современном мире её называют числом Эйлера :).
Чтобы не пропустить новые статьи, подпишись на мой телеграм-канал.